平衡车直立算法:互补平衡滤波
——结合加速度计和陀螺仪的平衡解决方案
Adapted from Shane Colton, The Balance Filter.
翻译 + 改编 by肥叉烧
Contents
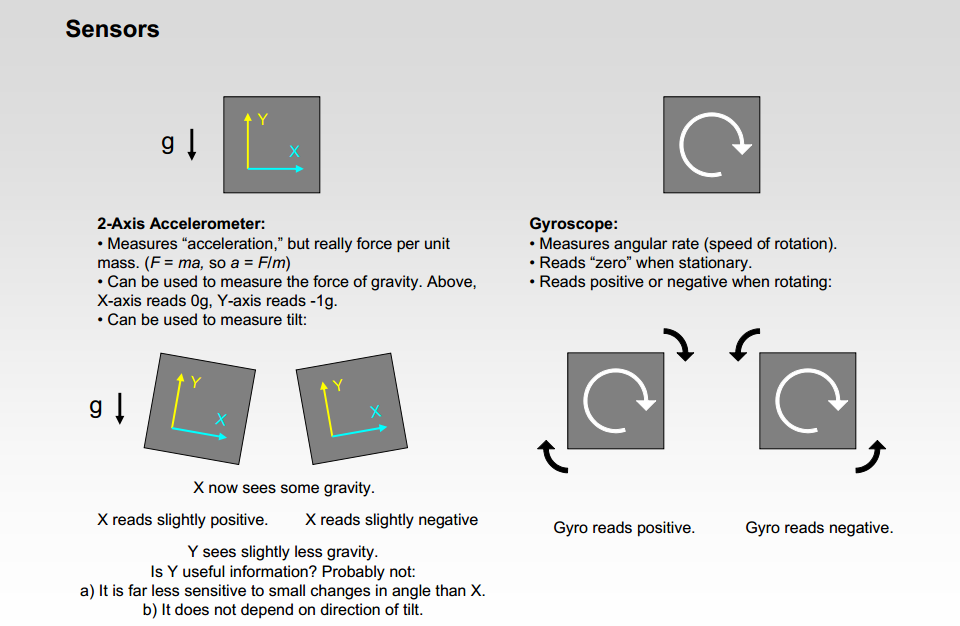
传感器
两轴加速度计
1. 用于测量“加速度”,但实际是测量单位质量上的受力。(F = ma,于是有a = F/m,牛顿就这么一说~)
2. 可用于测量重力,如上图,X轴的读数为0,Y轴的读数为-1g.
3. 可用于测量倾斜度:如上图,这时X轴和Y轴都有读数,通过简单的三角函数计算,就可以算得当前的倾斜度。(嗯,高中的我一定能轻松算出来~)
陀螺仪
1. 用于测量“角速度”(旋转的速度)。
2. 静止时读数为0.
3. 旋转时,读数是正数或者负数:与陀螺仪方向一致读数为正,否则为负。

从传感器中读数
首先,要用ADC(模拟/数字转换器)读出每个传感器的电压值,并将其转换成你用得着的单位。(如果懒得转换,可以自己创造一个新单位,比如1叉烧 = 212 电压读数)
要将电压值转换成可用的单位,你需要找到:
1. 偏移(offset):让陀螺仪静止,加速度计保持水平并静止(亦即Y轴上不受外力),这时候读到的电压值,就是偏移值。如果读数不稳定,取平均值即可。偏移值建议以signed int类型进行存储;
2. 转换系数(scale):传感器输出电压值乘上这个系数,可以得到我们想到的单位。这个系数可以在传感器的数据手册(datasheet)中找到,不怕折腾的话最好通过实验测得。
数字加速度计:实际上,我组使用的是数字加速度计,MMA8451,不需要ADC,直接用IIC协议读取测量值。数字加速度计的好处是可以对它进行各种配置,以获得更适合实际情况的读数(比如内置的数字低通)。坏处是,IIC真心很难读,当时用的底层还有bug,折腾了一个通宵才解决;(当然,解决之后就爽歪歪了)
关于加速度计,你还应该知道...
1. 如果你想要测出360度范围的旋转,有Y轴帮忙效果会更好,但Y轴并不必要;有Y轴和X轴的值,我们就可以用反正切函数求出角度值。没有Y轴,我们还是可以通过sin或cos以及X轴的值,求得角度值,毕竟重力加速度我们是知道的。不过,用sin或cos来求精确角度值,是妥妥的谋杀处理器(用DSP模块来解决也是个不错的选择)。
2. 对于平衡车,实际测量的角度大多是接近垂直的。(正常运行的情况下几乎是直立的,大概没人会拿它作电动秋千) 如果平衡直立车在某个方向倾斜了超过30度,估计控制器会马力全开地把它掰回来。在30度的倾斜范围内,我们可以用“小角度近似”定理和X轴的值来得到近似的角度值,从而节省处理器资源,减少代码复杂度。
在小角度倾斜且静止的情况下:
由于角度theta很小,可以近似 sin(theta) = theta; 在 theta = ±30°范围内有效;
在下述代码中,如果转换系数(scale)设置成:X轴指向垂直向下时,scale = 1(g)。那么得出的x_acc的单位,就应该是弧度(radians);
乘上180/pi,可以把角度转换成弧度。
需要的测量数据
要控制平衡直立,需要得到平衡车当前的角度和角速度,它们是PD控制算法的基础。PD控制的公式:
我们先不用管“电机输出”具体干些啥,它的基本思路是:通过PD的相互控制,使平衡车表现稳定。
实际中,PD控制就像在平衡车中加上可调的弹簧和阻尼:倾斜时,弹簧把车掰回来;弹簧过冲时,阻尼把弹簧的力消除掉;
再打个比喻:当我们推开麦当劳的门(拉推都可以打开),门上的弹簧就会自动将门往回拉。然而,门不是立刻能关上,而是来回摆动。这时候,门框的摩擦力(亦即阻尼),会慢慢将门的晃动速度减弱,晃动几下之后,门就顺利关上了。
计算角度和角速度
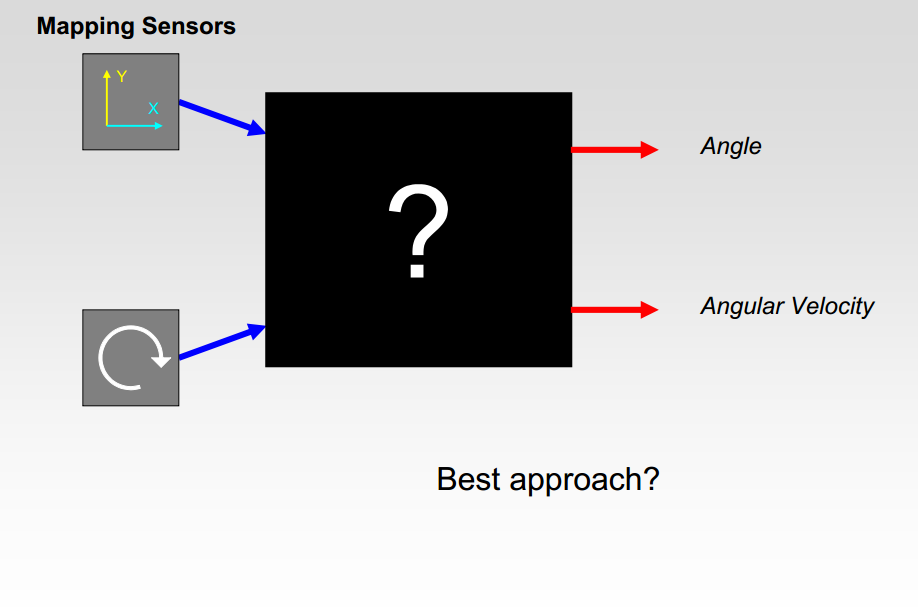
运用加速度计和陀螺仪,我们怎样得到平衡车当前的角度和角速度?
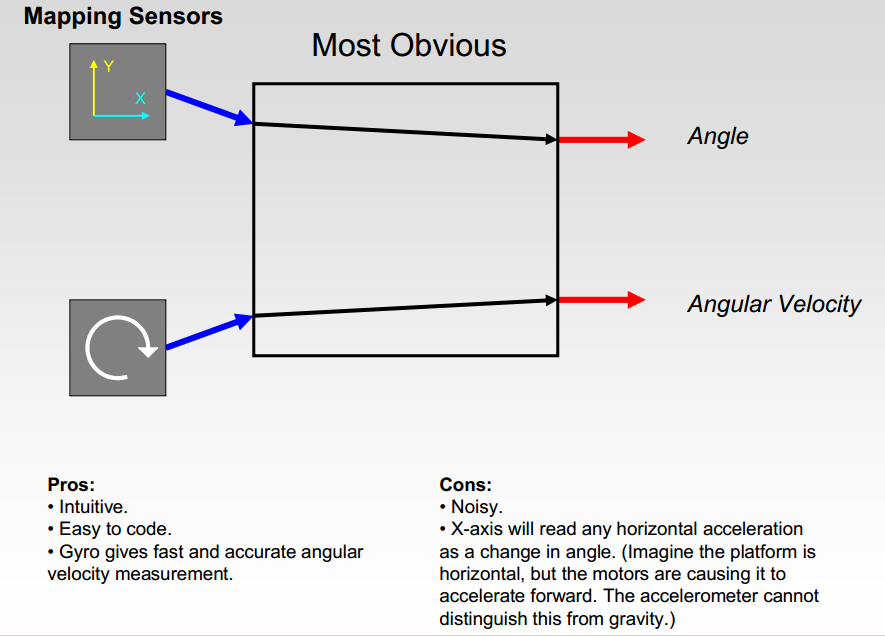
最明显的方法
显然,加速度计可以直接读出角度,陀螺仪可以直接读出角速度。
优点:
1. 直观,很直观,非常直观;
2. 写代码相当省事;
3. 陀螺仪能快速给出准确的角速度值;
缺点:
1. 噪声特别大,谁用谁知道;
2. X轴读数还会受到平衡车自身运动的影响;(只用Y轴的话就没事~)
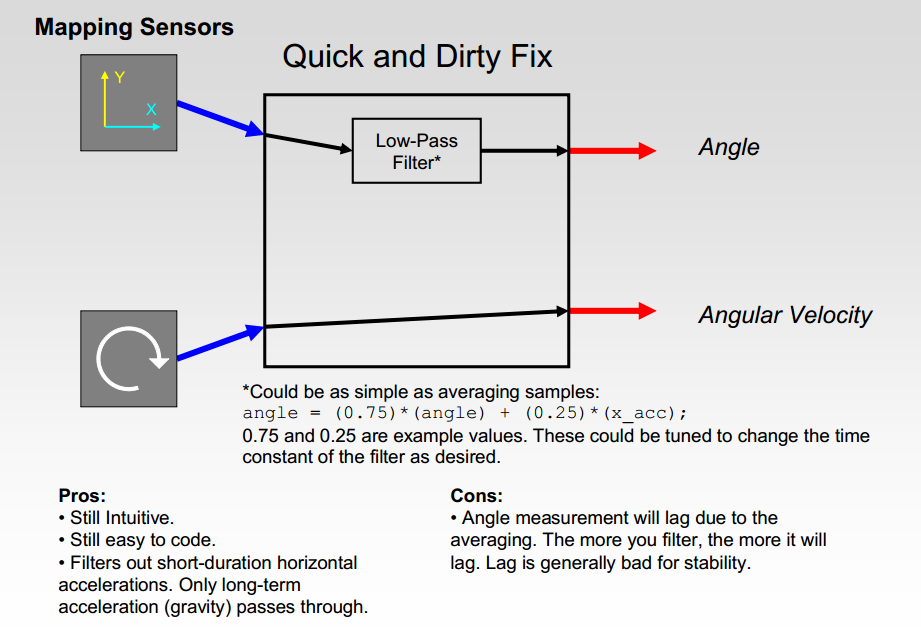
简单粗暴的解决方法
加速度计通过低通滤波器后得到当前角度值,陀螺仪直接输出角速度。
优点:
1. 仍然很直观;
2. 代码还是很简单;
3. 滤掉短时间变化的角速度,只有持久的加速度(重力加速度)可以通过。
缺点:
1. 角度测量会有所滞后;取平均的数量越多,滞后越严重;
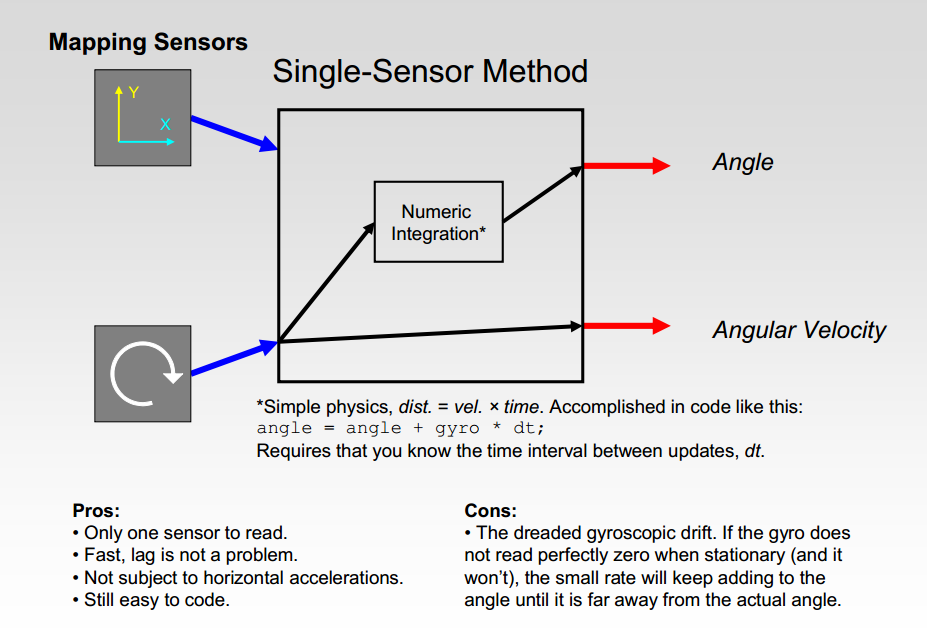
单传感器方法
只使用陀螺仪,直接从陀螺仪得到角速度,角速度对时间积分得到角度;
优点:
1. 只需用一个传感器;
2. 快速,不用担心滞后的问题;
3. 跟水平加速度断绝了关系;
4. 代码简单;
缺点:
陀螺仪存在温漂。如果陀螺仪在静止的时候,读数不是绝对的0,那么这一点点的偏移在长时间积分后,得出的角度与实际角度相差巨大;(失之毫厘,差之千里?)
卡尔曼滤波(Kalman Filter)
一般人看不懂的牛逼算法。
优点:
1. 理论上绝佳的算法,平衡算法中的战斗鸡,噪声什么的根本不是它的对手;
2. 连平衡车的物理属性都考虑上了;
缺点:
1. 一般人看不懂,技校学生更是无能为力;
2. 数学上复杂,需要用线性代数;
3. 代码复杂;
4. 耗费处理器资源;
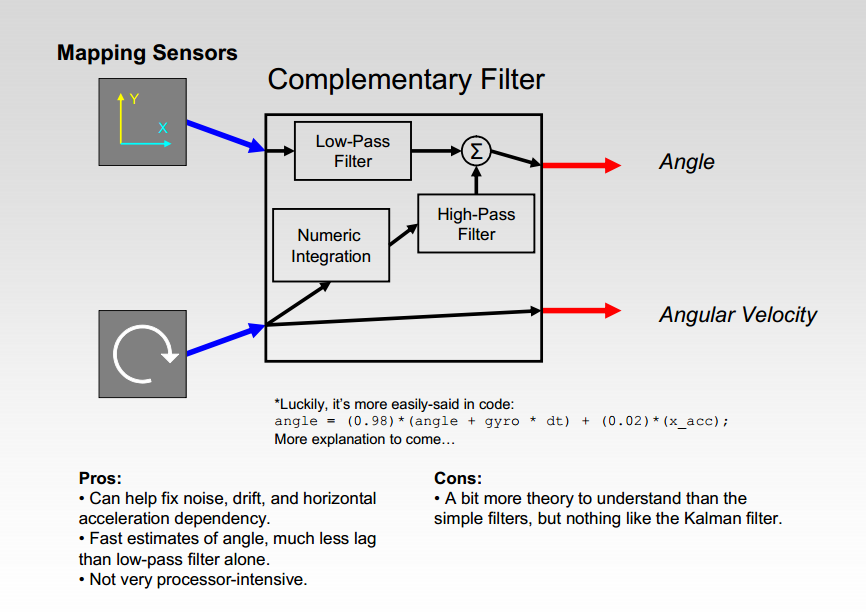
互补滤波
结合加速度计的准确性,和陀螺仪噪声小的特性,互取所长。
核心算法:
angle = 0.98 * (angle + gyro*dt) + 0.02 * (x_acc); // 0.98和0.02是随便取的数,后面解释;
优点:
1. 噪声、温漂、水平加速度,都不算事儿;
2. 快速得到当前角度值,滞后比低通滤波的少;
3. 处理器负担少;
缺点:
比简单滤波稍微复杂一些,但比卡尔曼滤波简单得多;
数字滤波器
数字积分
实际单片机用的积分,其实就是个累加;
设采样间隔为dt,每次采到的角速度值是gyro,那么,
角度可以这样得到: angle += gyro * dt;
低通滤波器
低通滤波目的是,保留长期变化,滤掉短暂变化。那么,让信号一点一点起作用而不是一下子猛烈作用,即在时间范围上取平均,问题就得到解决了:
angle = 0.98 * angle + 0.02 * x_acc; // x_acc是加速度计的实时角度值;

高通滤波器
数字高通滤波器,不那么容易解释,它跟低通滤波器是刚好相反的:除去长期变化,保留短暂变化。高通滤波器加于陀螺仪,可以滤掉温漂;
采样周期
程序每次大循环用的时间,下面标记为dt;
时间常数
时间常数用来定义滤波器对信号的作用;对于低通滤波器,信号长度比时间常数持久的,可以通过滤波器;对于高通滤波器,信号长度比时间常数短的,可以通过滤波器;对于一个数字滤波器:
时间常数tau可以这样计算:
所以,当你知道了要用的时间常数,就可以通过上述公式得到滤波器的系数a;
互补:互补意味着滤波器的两个部分的和总为1,以确保得到的结果是准确的,也使得线性估算变得可行;这里用到的角度互补滤波,并不是完全“互补”,不过得到的结果还能满足我们需求。
深入了解角度互补滤波
可能你会问,为什么要在 (angle + gyro*dt) 这里直接加上角速度积分。我就不告诉你了,try to figure it out!
如果这里滤波器的循环频率时每秒100次(亦即循环周期 = 0.01s),那么上述公式的时间常数就是:
这个时间常数确定了陀螺仪和加速度计的信任边界。信号时间周期低于半秒时,陀螺仪占主导地位,加速度计的噪声除掉;信号时间周期大于半秒时,加速度计的角度平均值就占据主导地位,有温漂的陀螺仪可以站一边去。

实验,是检验时间常数的标准之一。
首先你要挑一个时间常数,然后算出滤波器的系数a,弄到代码中去。
检查角度拟合曲线,如果拟合角度与实际角度总相差那么2°,就说明陀螺仪的温漂影响较大,你可能需要把时间常数设置到1s以下,来保证加速度计能尽快校正陀螺仪的温漂值。不过,时间常数越短,就意味着加速度计的噪声更容易通过。所以,你需要认真进行取舍,正所谓,鱼与熊掌不可兼得,老板来份熊掌味烤鱼。
计算正确的滤波器系数,尤为重要。这里再演示一次,比如,我设定时间常数为0.75s,程序的循环周期是26.2ms,那么滤波器系数a应该这样求:
于是,角度应该这么得到:
总结
讲了一大堆,核心算法就两条:
1. 要实现平衡,需要进行平衡PD控制。
平衡控制:
2. 为了准确控制,需要准确低噪及时的角度值和角速度值。采取互补滤波,取加速度计的准确,取陀螺仪的快速和稳定,得到好用的角度值。
角度拟合:
a = tau / (tau + dt)





很有用,谢谢!
嗯嗯 多交流
Arduino读取I²C上的MPU6050可以使用自带的算法?另卡尔曼滤波的Ard代码库已经有牛人编好开源了。