肥叉烧 feichashao.com

　　图像经过分块、DCT变化，已经为压缩作好准备了。纳尼！折腾了大半天才算“作好准备”，你大爷逗我吧？客官请息怒，“量化”就正式开始压缩啦，3天瘦20斤，效果显著，无用退款！

JPEG量化：更多地保留低频信息

　　经过DCT变换后，图像低频部分都集中在左上角，这部分信息对人类理解图像内容非常重要；图像高频部分集中在右下角，这部分记录图像的细微变化，人眼几乎不能察觉。
　　所以，更多地保留DCT左上方的低频信息，去除DCT右下方的高频信息，既能大大压缩图像大小，同时较好地保证了图像质量。
　　说得容易，实现方法也很容易，那就是“量化”。

　　Soga！那...量化是啥？
　　简单地说，“量化”是将“连续量”转换为“离散量”的过程。“四舍五入”、“向下取整”就是典型的量化。
　　比如，设量化器(Quantizer)为8，那么，16,21,24,59的量化结果是：
　　[16/8] * 8 = 16;
　　[21/8] * 8 = 16;
　　[24/8] * 8 = 24;
　　[59/8] * 8 = 56;
　　( 这里[ ]表示向下取整 )
继续阅读“[Week2.5]图像量化——JPEG在此压缩”

均方差(Mean Square Error, MSE)

　　评价一幅图像压缩前和压缩还原后的差异，有两种常用方法：
　　①大家来找茬——进化程度高的人类可轻易识别；
　　②数学方法——压缩前和还原后的图像作均方差；
均方差计算方法：

显然，MSE越小，图像的质量越好。

K-L 转换：

　　要想获得最小均方差的转换，可以使用K-L转换。K-L转换(Karhunen-Loève Transform)是建立在统计特性基础上的一种转换，它是均方差(MSE, Mean Square Error)意义下的最佳转换，因此在资料压缩技术中占有重要的地位。K-L转换是对输入的向量x，做一个正交变换，使得输出的向量得以去除数据的相关性。
　　简单地说，只要能不辞劳苦地算出图像的K-L转换，就能找到MSE最小的转换。
　　我的天啊，这听起来真棒！等等，K-L转换的计算复杂度奇高，半天压缩才压缩一副图片，恐怕自拍狂们会hold不住。
　　那有没有简单的变换方法，计算简单，又能保证图像质量？
继续阅读“[Week2.4]图像DCT变换”

JPEG分块对图像进行处理

　　JPEG压缩图像的第一步，是将图像分解成一个个8×8的小图像，之后再分别对这些小图像进行变换量化编码。

继续阅读“[Week2.3]JPEG采用8×8分块处理”

(笔记图片截图自课程Image and video processing: From Mars to Hollywood with a stop at the hospital的教学视频，使用时请注意版权要求。)

JPEG用哈夫曼编码(Huffman Encoder)作为其符号编码。哈弗曼编码是压缩算法中的经典，它理论上可以将数据编成平均长度最小的无前缀码(Prefix-Free Code)。

为什么要进行编码？

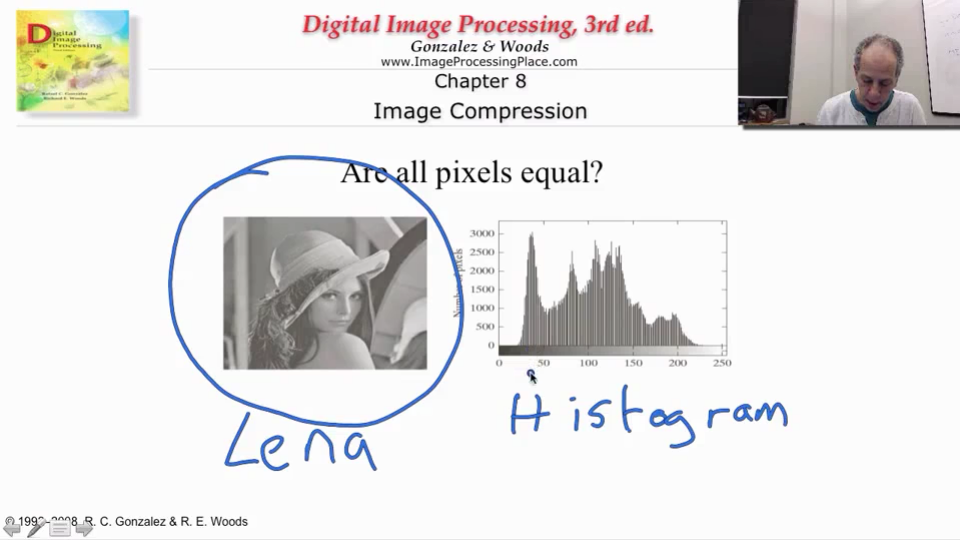
关于Lena：莱娜图（Lenna）是指刊于1972年11月号《花花公子》（Playboy）杂志上的一张裸体插图照片的一部分，是一张大小为512x512像素的标准测试图。该图在数位影像处里学习与研究中颇为知名，常被用作数位影像处里各种实验（例如资料压缩和降噪）及科学出版物的例图。(几乎每一本图像处理相关的书都会出现这张图片~)
Lena的直方图(Histogram)：从Lena的直方图中可以看出，图片中每个灰度值出现的概率是不相同的。这里，中间灰度值部分出现的概率比较高，两边灰度值出现概率非常低。所以，如果每个灰度值都进行同样长度的编码，似乎就太浪费了。

继续阅读“[Week2.2]数据压缩之经典——哈夫曼编码(Huffman)”

图像和视频的压缩技术应用广泛，每天刷微博的图片，盗版回来的小电影，无一不用压缩技术。

压缩的必要性

　　某天陈老师要录动作大片，经过长期艰苦奋斗，他制成了这样一段视频：画面大小1000×1000pixel，24位真彩色，每秒30帧，时长2小时。
　　如果不进行任何压缩，存储这段视频需要1000*1000*24*30*60*120=5.184 ×1012 bit ≈ 648GB的空间。(2014年4月5日,500GB硬盘最低价格是299元~)
　　用4M宽带下载这部大片，最少需要360小时 = 15天。
　　可见，要保障人民群众的切身利益，压缩技术非常有必要。
继续阅读“[Week2.1]图像为什么非压缩不可？”